Sight deposits: optimising the ALM model

Delivery of a procedure and an application module calibrated by machine learning, making it possible to determine an optimal model (i.e. investment strategy) for the replacement of sight deposits, from the point of view of return/risk, in the Markowitz sense, asset/liability management joining asset management here.

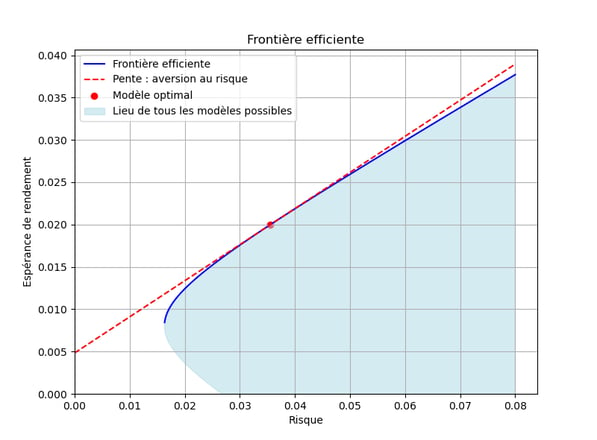
Extension of the Markowitz approach to Asset and Liability Management (ALM)

This very innovative approach

• restores a model's entire income trajectory,

• forces interest rate risk managers to propose only rationally admissible models (cf. efficient frontier),

• proposes a family of optimal models, requiring the calibration of a few parameters, which each month reproduce a replacement profile that depends on the entire prevailing yield curve,

• applies not only to current accounts, but also to interest-bearing savings accounts,

• can be applied to all products and lends itself to joint multi-product optimisation,

• makes it possible to explain a strategic choice in terms of risk appetite and the immobilisation of economic capital,

• puts leaders back to the heart of financial management, by giving them the means to choose a model once they have fully understood the risk/return implications of their decision.

Net interest margin on sight deposits

As this is often the largest component of a retail bank's Net Banking Income (NBI), we will systematically explore historical data and a wide range of hypothetical scenarios for interest rate curves and balance sheet outstandings,

• to assess the performance, in terms of risk/return, of its existing management strategies and models,

• situate them in relation to all possible strategies,

• consider abandoning them in favour of strategies that are more profitable, less risky and based on simpler, more robust models, while complying with regulatory constraints and the availability of hedging instruments.

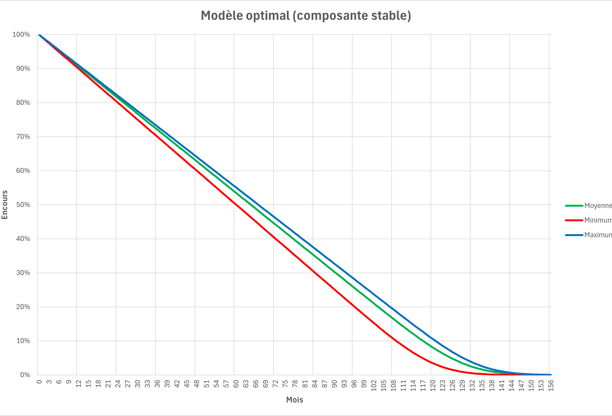
Example: French household sight deposits